📝 Overview
The Cryptarithmetic Puzzle Solver is a Python-based tool designed to solve cryptarithmetic puzzles where letters represent digits. The objective is to replace each letter with a unique digit such that a given arithmetic equation (usually addition) holds true. The solver brute-forces through possible combinations of digits to find all valid solutions.
The solver uses a brute-force search approach:
- Generates all possible permutations of digits (0-9) that can replace the unique letters in the puzzle.
- Applies these permutations to check if the resulting arithmetic operation holds true.
- Prints the valid mappings of letters to digits when a solution is found.
- Each letter is mapped to a unique digit.
- The first letter of any operand or result cannot be mapped to zero.
- Solves any cryptarithmetic puzzle with up to 10 unique letters.
- Returns all possible solutions where the puzzle constraints are satisfied.
- Handles puzzles with two word-based operands and one word-based result.
Ensure that you have Python 3 installed on your system. This project does not require any external libraries.
- Clone the repository or download the script.
- Run the script using the following command:
python cryptarithmetic_puzzle_solver.py3. When prompted, enter the two words representing the operands and the result word.
def solve_crypt_puzzle(word1, word2, result):
# Generate a set containing all the characters used in the puzzle
letters = set(word1 + word2 + result)
# If the number of unique characters is more than 10, the input is invalid
if len(letters) > 10:
print("Invalid input: More than 10 unique characters")
return
# Iterate over all permutations of numbers from 0 to 9
for perm in permutations(range(10), len(letters)):
# Create a mapping between characters and numbers
mapping = dict(zip(letters, perm))
# If 0 is assigned to the first character of any word, it's not valid
if mapping[word1[0]] == 0 or mapping[word2[0]] == 0 or mapping[result[0]] == 0:
continue
# Convert each character to a number
val1 = sum(mapping[char] * (10 ** (len(word1) - i - 1)) for i, char in enumerate(word1))
val2 = sum(mapping[char] * (10 ** (len(word2) - i - 1)) for i, char in enumerate(word2))
res = sum(mapping[char] * (10 ** (len(result) - i - 1)) for i, char in enumerate(result))
# If the operation satisfies the condition, print the mapping and visualize it
if val1 + val2 == res:
print(f"Solution found: {word1} + {word2} = {result}")
for letter, value in mapping.items():
print(f"{letter} = {value}")
# Visualize the mapping
visualize_mapping(mapping)
print()
# Input from the user
operand1 = input("Enter line 1> ").upper()
operand2 = input("Enter line 2> ").upper()
result = input("Enter line 3> ").upper()S = 9 E = 5 N = 6 D = 7 M = 1 O = 0 R = 8 Y = 2

def visualize_mapping(mapping):
"""Function to visualize the mapping of letters to digits using a bar chart."""
df = pd.DataFrame(list(mapping.items()), columns=["Letter", "Digit"])
df = df.sort_values(by="Letter") # Sort by letter for better visualization
# Plot a bar chart to visualize the mapping
df.plot(kind="bar", x="Letter", y="Digit", legend=False)
plt.title("Letter to Digit Mapping")
plt.ylabel("Digit")
plt.xticks(rotation=0)
plt.show()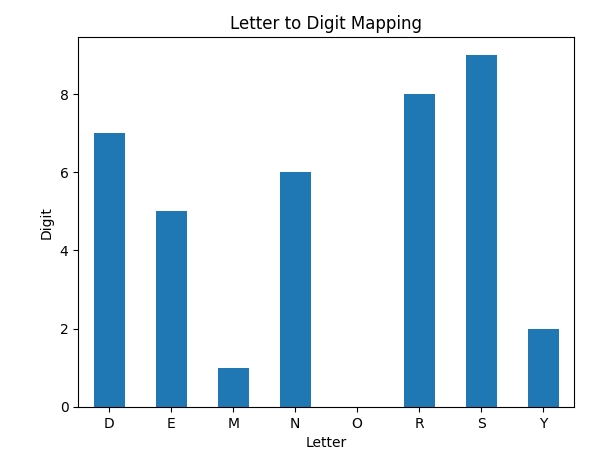
- Input Parsing: The puzzle words are treated as numbers, with unknown digits represented by letters.
- Letter Set Creation: A set of all unique letters is created from the input operands and result word.
- Permutation Generation: The solver generates all possible digit permutations for the letters.
- Validation: The program checks if any of the generated permutations satisfy the condition word1 + word2 = result.
The solver only supports puzzles with a maximum of 10 unique letters due to the digit constraint (0-9). The solution might take time depending on the number of unique letters, as the number of possible permutations grows exponentially.
- Clarity in headings: Section headings are made more descriptive for easier navigation.
- Expanded explanation in “How It Works”: Added clearer explanations of each step of the solver’s operation.
- Enhanced formatting: Improved formatting for better readability.
- Incorporated your sample output: Included the example output and image for better context.