Sudoku Solver Using Backtracking Algorithm

This project implements a Sudoku solver using a Backtracking algorithm. The solver attempts to solve Sudoku puzzles by filling in empty cells one by one, checking whether each entry is valid, and backtracking when it encounters invalid configurations. The project is implemented in Python, with additional helper functions to handle board input/output, validation of moves, and display of the Sudoku grid.

🚀 Key Components:

1. Board Representation

The Sudoku board is represented as a Python dictionary, where each cell is accessed by a key in the form of ‘A1’, ‘B2’, etc., where the first letter corresponds to the row and the second digit to the column.

2. Print and String Conversion Functions

print_board(board): Displays the Sudoku board in a human-readable 9×9 grid format.
board_to_string(board): Converts the board’s current state into a string format for saving or further processing.

def print_board(board):# Prints the Sudoku board in a square grid.
    print("-----------------")
    for i in ROW:
        row = ''
        for j in COL:
            row += (str(board[i + j]) + " ")
        print(row)

def board_to_string(board):#Converts the Sudoku board dictionary to a string for writing.
    ordered_vals = []
    for r in ROW:
        for c in COL:
            ordered_vals.append(str(board[r + c]))
    return ''.join(ordered_vals)

3. Move Validation

is_valid_move(board, row, col, num): Checks if placing a given number in a specific cell is a valid move according to Sudoku rules (row, column, and 3×3 grid checks).

def is_valid_move(solve_board, row, col, num):
    # Check if the same number appears in the same row
    for x in range(9):
        if solve_board[ROW[row] + COL[x]] == num and x != col:
            return False

    # Check if the same number appears in the same column
    for y in range(9):
        if solve_board[ROW[y] + COL[col]] == num and y != row:
            return False

def is_valid_move(solve_board, row, col, num):
    # Check if the same number appears in the same row
    for x in range(9):
        if solve_board[ROW[row] + COL[x]] == num and x != col:
            return False

    # Check if the same number appears in the same column
    for y in range(9):
        if solve_board[ROW[y] + COL[col]] == num and y != row:
            return False

4. Backtracking Algorithm

solve_sudoku(board, row, col): Recursively attempts to fill the board using backtracking. If a valid configuration is found, the puzzle is solved. Otherwise, it backtracks by resetting the current cell and trying different values.

def solve_sudoku(sudoku_board, row, col):
    #The solve_sudoku function performs backtracking recursively to solve the Sudoku puzzle.: BackTracking

    # Check if we have reached the last row and column, indicating completion of the puzzle
    BOARD_SIZE = len(ROW)
    if row == BOARD_SIZE - 1 and col == BOARD_SIZE:
        return True  # Return True indicates a successful backtracking

    # Move to the next row if the current column has reached the end
    if col == BOARD_SIZE:
        row += 1
        col = 0

    # If the current cell is already populated, move to the next column
    if sudoku_board[ROW[row] + COL[col]] > 0:
        return solve_sudoku(sudoku_board, row, col + 1)

    # Try placing numbers from 1 to 9 in the current empty cell
    for num in range(1, BOARD_SIZE + 1):
        # Check if it is valid to place the number in the current position
        if is_valid_move(sudoku_board, row, col, num):
            # If it's valid, assign the number to the current cell
            sudoku_board[ROW[row] + COL[col]] = num
            # Recursively try to solve the puzzle for the next column
            if solve_sudoku(sudoku_board, row, col + 1):
                return True
            # If the puzzle cannot be solved for the next column, backtrack by resetting the current cell to 0
            sudoku_board[ROW[row] + COL[col]] = 0

    # If no number leads to a valid solution, return False, indicating that the puzzle cannot be solved with the current configuration
    return False  # Return False indicates failure

5. Board Solving

backtracking(board): Solves the given Sudoku puzzle using the solve_sudoku() function. It also prints whether the puzzle was successfully solved or not.

def backtracking(board):#Takes a Sudoku board and returns the solved board using backtracking algorithm.
    # Create a copy of the board to prevent modifying the original board
    solved_board = board.copy()
    # Attempt to solve the Sudoku puzzle
    if solve_sudoku(solved_board, 0, 0):
        print('Solved')
    else:
        print('Unsolved')
    return solved_board

🛠️Running the Sudoku Solver

Single Puzzle Mode

To solve a single Sudoku puzzle, provide a string of 81 digits (representing the puzzle) as input via the command line:

python3 sudoku.py "530070000600195000098000060800060003400803001700020006060000280000419005000080079"
python3 sudoku.py

📝Example:

Conclusion

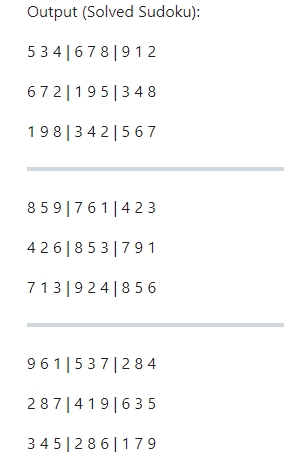
This project demonstrates how a backtracking algorithm can efficiently solve Sudoku puzzles by exploring all possible configurations, validating each move, and adjusting dynamically when an invalid configuration is encountered. The program supports both single-puzzle and batch processing modes for convenience.

gksdusql94/AI_Sudoku (github.com)

Tags: Artificial Intelligence Games